Height measurements

Equipment needed

You only need three pieces of equipment to properly measure a tree: a measuring tape, a calculator (with cosine and tangent functions), and an inclinometer to measure angles.  If purchasing an inclinometer (Abney level, clinometer, etc.) is beyond your budget, or you can’t borrow one, there are mobile phone apps that allow you to use a smartphone as an inclinometer. Here are two possible options: Smart Measure and iHandy Carpenter.  See Gabriel Hemery’s helpful instructions on using iHandy Carpenter to measure tree height.

Today Foresters use a Hypsometer – an all in one tool that measures distance, angles and even calculates tree height for you.  This equipment hastens the measurement process, but it is not necessary.

For fun!

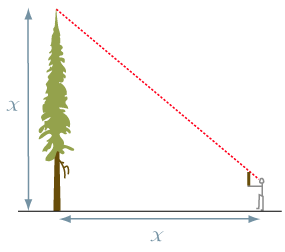The stick method- how they built the pyramids!
This old but simple method only works on level ground.  It just requires a stick and a distance measuring tape.  The stick must be the same length as your arm or grasped at a point where the length of the stick above your hand equals that of your arm.  The stick is held pointing straight up, at 90 degrees to your outstretched, straight arm.  Carefully walk backwards until the top of the tree lines up with the top of your stick.  Mark where your feet are.   The distance between your feet and the tree is roughly equivalent to the height of the tree.  You might find it interesting to compare your results using this simple method with the standard methods described below.

How to measure height

Height is the hardest measurement to take accurately, especially for larger trees. Measurements become more reliable the greater the distance you are from the tree (the distance you are away from the tree must be greater than the total tree height).  In dense forests it can be challenging to get a clear view of the tree top.  The slope of the ground can also make measurement difficult.  Trees that are leaning significantly should be measured with the lean to the right or left, not with the lean toward or away from you.   In challenging forest situations we recommend making more than one attempt to measure height.  If possible try and remeasure from a different view point, and always double check your measurements.

The math used in height calculations

Working on level ground
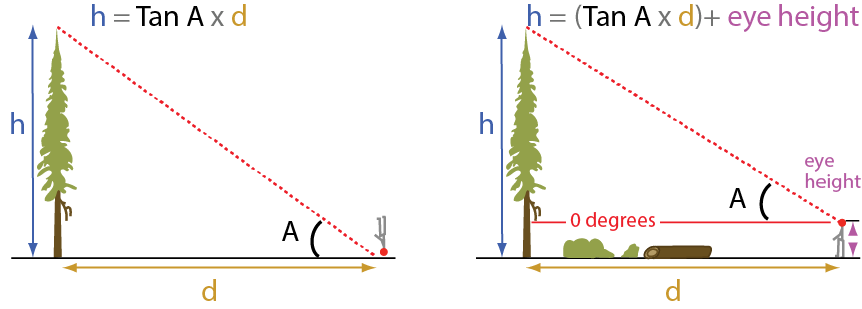
Calculating tree height requires the use of basic trigonometry: h = Tan A x d, where h is the tree height, d is the distance from tree, and A is the angle to the top of the tree.  Since your measurements will be made at eye level, you need to know your eye height (height of your eye above the ground). The equation then becomes h = Tan A x d + eye height.

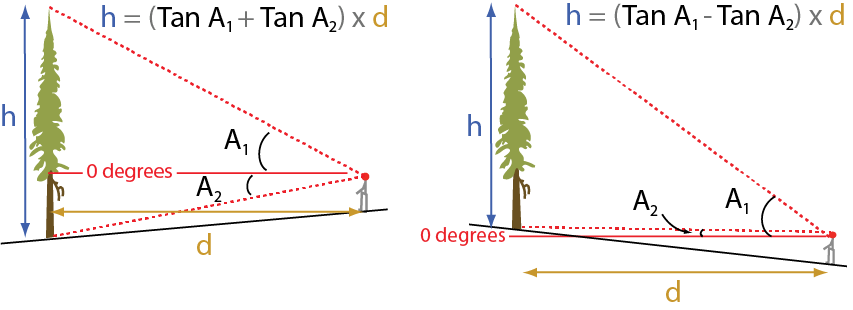
Working on moderately sloped terrain
If the only option available to you is to stand either up or down slope of the tree, and the gradient is such that the base of the tree is above or below eye level, additional angles need to be measured.   In addition to tree top angle, you need to measure the angle to the tree base.  These angles are either subtracted or added depending on whether you are above (added) or below (subtracted) the tree.

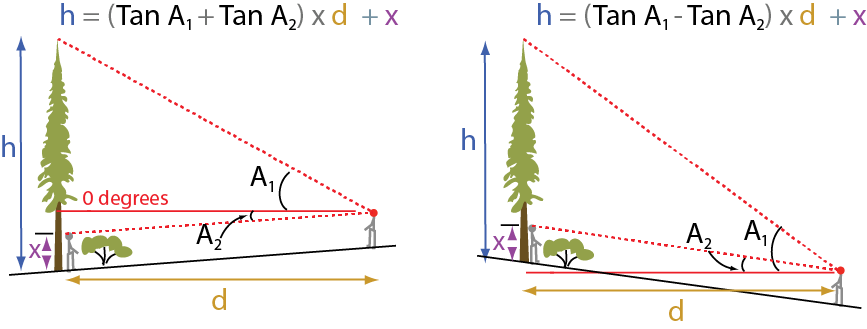
Tree base is obscured or hidden from view
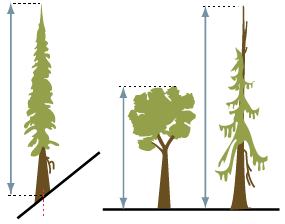
Often obstacles such as shrubs, rocks, or fallen trees can obscure the tree base from view. In this case, you will need to measure the angle to a mark on the trunk that is a known height from the ground. One method, shown in the illustration below, is to have someone stand at the base of the tree and measure the angle to the top of their head (height x). If you can’t see them through the tall bushes, try having them hold a flag or bright coloured stick above their head at a known height.

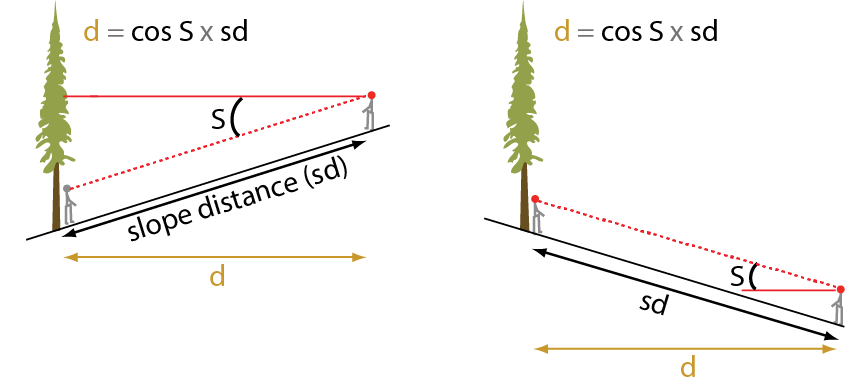
Working on steep terrain
On very steep terrain it is almost impossible to accurately determine your horizontal distance from the tree. In situations where the ground is sloped (up or down) more than 6 degrees (10% slope) you will need to measure slope distance. Once you measure slope angle and slope distance, horizontal distance can be calculated.